(Edited transcript of a videoconference keynote address given at IMS 2005.)

It is a pleasure to be with you all today. My main excuse for not being there in person is that we really have to finish the next version of Mathematica. I think it is probably fair to say that almost nobody thinks I should be doing anything other than working very hard on the upcoming version of Mathematica, which I can assure you is going to be something extremely exciting, that we have been working on for a great many years.

But I thought today that I would not talk mainly about near-term Mathematica technology. The original title for this talk was Mathematica and the Future of Computation, but then I saw it had been changed to just The Future of Computation. The modification to the title got me thinking about what I really should be talking about. So I am going to talk about the modified title. I decided that would give me more license to talk about a broader range of things, and I thought that we might have some fun with that.

What will be the future of computation? To really home in on that question some of what we have to think about is what computation is, what computation has been, what kinds of things could computation be in the future, what kinds of things can we perhaps uniquely learn from our experience with Mathematica about the nature of computation and about its future directions.

As far as I am concerned the essence of computation is the idea of finding an abstract representation for processes, processes of some kind or another. In a sense, if you look back at the far distant history of computation there were sort of programs of computation in antiquity, in Greek times. People were talking about how you could represent any human language. All the different ideas that existed in the world you could represent using this limited grammar of a human language. And that was a kind of program of computation, of being able to build up all possible concepts from this limited set of grammatical rules.

Then much later, people like Leibniz in the late 1600s were talking about the idea of mechanicalizable, universal language. In his case, his business was being a diplomat, so he was interested in finding a mechanical way to make his life easier, so to have a machine be able to determine the truth or not of any human proposition. He came up with this idea of mechanizing the process of finding out whether things were true and inventing a kind of universal language to determine that.

He did not get terribly far with that and it was another few hundred years before more progress was made. I guess the next major step in the development of the notion of computation came with the formalization of mathematics. Mathematics in its earlier days had been in a sense very practical. In ancient Babylon it was about doing arithmetic for purposes of commerce or doing geometry for purposes of land surveying. In the development, things got a bit more abstract—the invention of algebra in the 1500s, the idea of symbolic variables, variables that could stand for arbitrary quantities, things like this.

But I guess it was during the 1800s the idea of purely abstract kinds of mathematical constructs and operators really took root. There were things like the work of Galois on groups and the development of Boolean algebra and abstract logic by Boole. Then came the development of abstract algebra in the late 1800s and so on. Then there was the notion of people like Peano trying to formalize, trying to make a human-like language that could be used to find a uniform formalization of mathematics. And that, in the 1910s, led to things like the Whitehead and Russell venture of Principia Mathematica, one of the uses of the “mathematica” word in the past, where the notion was could one take all of the ideas of mathematics and formalize them in a way that was somehow based on logic? As you may know, Whitehead and Russell produced this giant three-volume work that purported to describe how mathematics worked. Unfortunately, it went in rather small steps and it was rather hard to understand. It determined that 2 + 2 was equal to 4 somewhere about two-thirds of the way through the first book. It was an early attempt to formalize a process, in this case a process of mathematical proof and presentation.

When you look at the pages of Principia Mathematica they almost seem like a uniquely bad notation for actually presenting the ideas of mathematics. Nevertheless, as a proof of principle it was something very important to take this large volume of potential mathematical knowledge and try and formalize it in a uniform way.

Then there were other kinds of ideas that came up in the 1920s about the formalization of things. For example, the idea of recursive functions came up. In fact the very idea of functions had been a fairly recent construct, something that had really cropped up in the 1880s or so. The idea of just some abstract thing, of , where you feed it anything and it munches on it and produces an answer. That idea of abstracting a notion of a function was a comparatively late one in the history of mathematics.

Then there was the question of what were the elements out of which you could build these functions? So an idea that came up in the 1920s was maybe we can make recursive functions. Maybe we could build up any function that we cared about. People talked about the operation of primitive recursion, which involves things like successor operations, where the value of a function depends on previous values of that function, essentially things that will fix do loops and so on.

Then various developments happened. I think in 1925 it was realized that there were functions that were admittedly rather poorly constructed, things like the Ackermann function, that seemed to be mathematical in character, yet could not be represented as a primitive recursive function. That was one attempt to completely formalize the idea of functions and processes, the primitive recursive functions. That attempt did not work out. It turns out that things that seemed like they were decent, sensible mathematics-like abstract constructs could not be formalized in terms of primitive recursive functions.

Then there came general recursive functions and by about 1930 that began to take root. They got used in a serious way in the proof of Gödel’s theorem in 1931. It is a technical side corner of Gödel’s theorem to use these general recursive functions, but it was an important technical development. What then ended up happening was that it was realized that between the general recursive functions, the idea of lambda calculus that had been introduced by Alonzo Church, and then the idea of Turing machines, that these were all attempts to formalize the notion of what processes can happen. On the one hand in Gödel’s theorem the processes that were being formalized were processes of mathematical theorem construction, so to speak. In the case of lambda calculus, it was something very much the same. In the case of Turing machines at first I think Alan Turing’s idea was to formalize what bank clerks do. That was his notion of what would be the raw elements of computation, which would then be the things that a mathematician might also do. He was also interested in applications to the foundational problems of mathematics.

The Turing machine idea was introduced in 1936. It was realized in the next few years that these different notions of abstract computation, these different building blocks that you could make a computation out of, were all ultimately equivalent. The notion of a universal computation that could be done using any one of these sets of building blocks was a fairly robust notion.

As time went forward, there were a few other strands, a few other kinds of primitive operations that were considered for computation. Another one that came very early in the history, although was ignored until many years later, was an idea called combinators, which are the ultimate functional programming construct, in a sense. These typically are set up as two combinators, and , and it is a nice Mathematica exercise to construct functions out of just nesting these and combinators. That was actually an idea that came up in 1921. Although it was not really recognized until probably the 1940s or later, that this was a significant and worthwhile thing, which has perhaps not even been recognized until today.

So this notion of computability had arisen of all these various different approaches to formalizing what were essentially mathematical-type, computational kinds of things. Those formalizations were in a sense based on symbolic constructs and nesting of functions and all these kinds of things. Then as the world moved forward and practical computers started to be built, many of the very early uses for computers were for what would now be considered data processing. IBM, for example, in its early days was dealing with census data. There were a few uses for things like ballistics and during the Second World War for things that we would view as being more like mathematical computation. But the main strand of computer development and information technology development tended to be this data processing idea, where the computational operations that had to be done were fairly straightforward. Even in the case of doing ballistics computations, the kinds of operations that you needed the computer to do were very much the traditional operations of mathematics.

If you have instead of a high school order of mathematics, if you look at combinators or something like that, you are dealing with these bizarre, abstract functional programming kinds of constructs. But nobody needed any of that in the early history of practical computing. It was either we are just dealing with data and fairly fixed formats—we are going to take these pieces out of this record and add them together and figure out which other records are the same kind of thing—or we are doing calculations with elementary Newton’s laws for ballistics or some such other thing.

So in the practical development of computing, although there were early efforts like LISP and so on to develop languages that really tied in to the early conceptual ideas about computation, the practical computer languages which developed tended to be more along the Fortran line, with the notion of fairly fixed operations based in traditional high school mathematics together with fixed data sets—fixed data structures—that could be pulled out of large databases that were collected for purposes of census data or standard kinds of financial data for companies and the like.

The idea of what computation consisted of became much more mundane in its practical application than it had been in its early history. As we go forward in the use of computation by the time one is getting to the 1980s, for example, there were other kinds of uses of computation, like word processing and later dealing with images. The typical thing that was happening was another modality, another kind of data was being attacked with computation.

When I got serious about building what is now Mathematica, one of the things that I was interested in was to see how general could we make this notion of computation. How could we take the idea of what computation could be, the representation of arbitrary processes and arbitrary kinds of constructs and to what extent could we build the system that could really make use of this potential generality that the idea of computation has?

What this led me back to was perhaps the earlier history of computation and particularly to what we now think of as symbolic programming. The notion of symbolic programming, the core idea of symbolic programming, is to say that everything can be represented symbolically. That means we can take the kinds of constructs that we deal with and we can represent every aspect, the operations on those constructs, the structure of those constructs, and so on, symbolically. That means we are not stuck with using a fixed data structure. We can allow the structure of the data as well as the content of the data to be manipulated, because everything we are dealing with is symbolically represented. So this generalizes our notion of what is possible to do with computation.

With this idea of symbolic programming, we can look at different territories, things that might be represented in computational terms whether they are algebraic formulas, whether they are pieces of graphics, whether they are document structures. And each one of these particular fixed structures we can very quickly, with symbolic programming, we can immediately go in and say we can now attack this territory as well because we are using the same uniform set of operations that we have used for all these different territories. But the greatest power in a sense comes from the interplay between all these different areas and being able to take this main thread of computation and go from one area to another using the underlying idea of abstract representation of processes, operations, data, and so on, in computational terms.

So this line of thinking is part of what got me started, what fueled some of my scientific efforts. For my own personal purposes, the idea that when one builds a computer language like Mathematica, in a sense what one is trying to do is take all these abstract processes that people want to do and find what the primitives are out of which those operations can be formed. And then we give those primitives names like NestList or Fold or whatever else. Those are the primitives from which we build up the things that people want to do—the processes that people want to carry out.

So my kind of idea—my kind of science idea of now 25 years ago—was, given that it seemed to work fairly well, to try and come up with what are the primitives that are relevant for some processes that people want to do. So the notion came up, can one find some primitives that are relevant for representing what nature does? And the traditional science idea in exact sciences has been, the idea for the last 100 years or so has been, okay, we want to represent what nature does, the right way to do that is using mathematical equations and ideas like calculus.

Before Newton, it was not clear how one should represent processes in nature. There were a lot of different sometimes quite wacky ideas about that, the great advance of 1687 and Newton’s Principia Mathematica, the title of his book was Mathematical Principles of Natural Philosophy. His notion was can we take natural philosophy, this systematic study of nature, and can we put mathematical principles onto that. That was a great idea and a great advance. It fueled the development of the physical and other exact sciences for 300 years, this notion that one can take mathematical equations, ideas from mathematics, ideas about calculus, and so on and one can use them to explain and represent processes in nature.

One of the issues that come up there, and one that I was very interested in, was that is a fine thing, there are many places where this kind of notion of representing things in mathematical terms works out really well, whether it is working out the orbit of a comet or something like that. There are also places where it does not work out so well, whether it is looking at the forms and patterns of flow in a turbulent fluid or whether it is looking at the forms of some biological organism or trying to explain something about linguistics or some such other thing. Those are places where this kind of traditional mathematical way of representing abstractly the processes of nature does not seem to work so well. So the question is: Can one do something better, can one extend this idea of abstractly representing the processes of nature, can one go beyond representing them in purely mathematical terms?

So in a sense, as I was saying at the beginning, at least my view of what computation is in essence, is that it is a way of finding an abstract representation of processes. So among other things these ideas of computation should be able to find good abstract representations of the processes that go on in nature too. What one realizes as one looks at the underlying constructs of whether it is Turing machines, whether it is Mathematica, the underlying as it is turned out quite uniform constructs that support universal computation that allow one to make programs and so on, all those constructs are considerably broader than traditional ones that exist in mathematics and arithmetic and calculus and so on.

And so the question that was the starting point, although I have to say I did not formulate it quite as clearly as this, the starting point or as it turned out historically the rather confused starting point for what I did 25 years ago or so now was this question of: If we can use arbitrary kinds of computational systems to represent nature, how might that work and might that work better than using the fixed set of constructs we have in traditional mathematics? So the thing that I got started on was saying: If we are going to do this, what are some examples of computational systems that we might look at? Then what we are confronted with there is being asked in very raw form: What are the possible computations, what are the possible kinds of abstract processes that we might like to consider? And so following traditional natural science form, I started off thinking: What are the simplest kinds of computational processes that one might try to study? And so I ended up in particular looking at these systems called cellular automata that I am sure you have all seen.

Figure 1 is an example of one of them.

Figure 1.

Figure 1 is just a cellular automaton that is a one-dimensional system. It is just a horizontal line of black and white cells. We started off with just one black cell at the top. At every step we colored a particular cell based on the colors of the three cells on the line above that touch it. In this particular case everything that happened is very straightforward. We just get a uniform black pattern.

But what we realized is that there is a general kind of rule that we can use to study these processes. We can represent what is going on here by saying for each possible arrangement of three cells on a particular step, what will be the color of the cell on the next step?

Then I asked: If we are looking at things like this, what happens if we just look at all possible rules that have that general form? In a sense, what we are doing here is we are saying, we have got this abstract notion of computation, there is a whole universe of possible abstract computations. Let us look at that universe of possible abstract computations and see what is out there.

Now we might have thought that if the computations were really simple that we would not ever see anything terribly interesting. And that is certainly what I at first assumed. I started generating this universe with line printers and got these kinds of pictures of what happens with all the different possible rules. There are 256 rules of the particular kind shown in Figure 2. What happens with all of those possible rules?

Figure 2.

Well many of them do really pretty dull things, like rules 0 and 8 start off with one black cell and everything dies out.

Or rules 2 and 4 start off with one black cell and you just get a stripe. But what you see is that they do not all do completely boring things.

Figure 3.

For example, as you get a little ways in you start seeing things like those in Figure 3. Where you start off with one black cell and you just follow that simple rule at the bottom and the pattern that you get is at least very intricate. When we look at this with some detachment, we realize that although it is intricate, it is in a sense very regular. It is a perfectly nested, perfectly self-similar pattern that we have got out from following those rules at the bottom there.

But if you looked at that picture of all the different possible rules, I think Figure 2 shows the first half of the 256 possible rules, if you just trace through all those rules, number 30 is my all-time favorite and Figure 4 shows what it does.

Figure 4.

So again here we are starting off with just one black cell at the top, we are following that rule shown at the bottom there, and the pattern of behavior that we are getting out is this thing here. That at least looks pretty complicated.

So you might think, well this is a really simple rule. Somehow I must be able to crush this rule. I must be able to see if I continue running this thing longer, if I use some fancy mathematical method or something, I might be able to see if really this is a simple thing.

Well keep running it a bit longer and Figure 4 is what you get. What you find is there is a certain amount of regularity you can see over on the left, for example. But in many respects this picture looks extremely complicated and in a sense seemingly random. In fact, for example as a practical matter, the randomness of this is sufficiently good that if you take the center column of this thing and you wrap it around in a finite-size register and all that kind of thing, you can use that center column as a way of generating randomness.

And in fact, the Random function in Mathematica, , has used this method for generating randomness ever since Mathematica Version 1 was released. And it has been a really good method of generating randomness. In fact it has been an embarrassment to us that for some real number random generation methods we used, against my better judgment I was convinced that we should use more traditional random generators, which were slightly faster at the time when these things were first implemented but which have turned out to have all kinds of horrible bugs. So, this particular way of generating randomness, this little rule 30 thing, which is by far the simplest in terms of its rule, has withstood all of these attacks. So this is a remarkable thing. It is not one’s common intuition.

One’s common intuition is if you want to make something complicated you have to go to a lot of effort. You have to carefully construct things and build your complicated engineering system to achieve the complex goals that you want to achieve. But what is happening here, and this is the remarkable thing that I first noticed back in 1984 although I did not really understand it with clarity until later, was that with this kind of rule, even though the rule is very simple, one can get behavior of great complexity out of it. And this is something, in a sense this is not like chaos theory where you still have wiggle room because you are still feeding in these real numbers which have an infinite number of digits or any of these other kinds of things where you are moving the information around but it always was there anyway.

Here really the only things you need to know to construct this picture are the rule at the bottom and the fact that you start with one black cell and you get out all this stuff. In a sense this is a very intuition turning kind of observation. It took me a long time to kind of get used to this. That when you look out in the computational universe very simple systems can produce extremely complicated behavior.

So the question is: Why have we not seen this before? The main reason we have not seen this before is that in our efforts to do engineering, to achieve tasks with computers and things like that, we tend to want to deal with systems where the systems are set up so that we can readily see what the system is going to do. We do our engineering on the basis of progressively setting up the pieces so that we can always foresee what the whole system is going to do.

Now of course, nature does not produce things that way. Nature just does what it does and what comes out is what comes out. And it seemed like, in the past, that there is sort of a secret in nature that allows it in what seems to be a quite effortless way to produce all kinds of complexity that we as humans find very hard to produce. For example, if you are showing two objects and one of them is an artifact and one of them is a natural system, it is a pretty good heuristic that the one that looks simpler will be the artifact. Because we do not typically know how to make things that look really complicated. We tend to make things that have simple circular structures or whatever else. That has been our practice of engineering.

But nature has a different kind of way of making things. And I think that much of its secret of making things has to do with what we are seeing in the case of this rule 30 system. If we look out there in the space of all possible abstract computations, a lot of them, even simple ones, have the property that they produce behavior of very great complexity.

So what does this mean for our understanding of nature, our understanding of computation, our understanding of technology, and for the title of this talk, the future of computation?

One of the things one might start to think about is: What does it mean to have a system that does a computation? Usually when we think of computation we think of setting a system up to specifically achieve some particular task that we have set for it. So for example, Figure 5 is a system, it happens to be a cellular automaton, that is set up specifically to achieve the task of squaring its input. So you put in black cells at the top and then the system does its thing and then out at the bottom by a not terribly clever algorithm the system produces squared black cells.

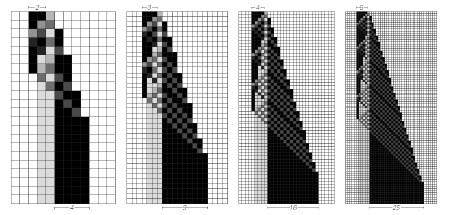
Figure 5.

So this is an example of a computation and you can have something slightly more elaborate.

Figure 6 is an example of a cellular automaton that is computing the primes.

Figure 6.

Again it does its computation over there on the right, using the standard sieve of Eratosthenes method. On the left you get stripes, which are at the positions of the primes.

So these are things, we kind of know they are computations because we kind of know what the point of them is. We set them up to be computations where we knew what the point was beforehand.

But the question is: When you see a system like Figure 7, does that validly count as a computation?

Figure 7.

Well, I think that the answer is really definitely yes, it absolutely counts as a computation. It is not a computation where we necessarily know the point of it beforehand, but it is a computation that just happens. It is a computation that perhaps may be happening in nature quite a bit. And it is a computation that sometimes we may find out is actually quite useful. Like in the case of this rule 30 system, it has been very useful as a random generator in Mathematica and elsewhere.

And so the question we might ask is: Is there something about this computation that is fundamentally weaker than the computations that we are used to doing in our CPU chips and all this kind of thing? And so for that we have to ask the question: Within this system, could we construct a computation, could we construct all those kinds of computations that we can readily do with a standard CPU chip? Can we make this system act like a universal system that can be programmed in the kinds of ways that our standard computers can be programmed?

There is a question then about the following thing, which is, one might have thought that it would be true that as we look at different kinds of computational systems, as we look out in the computational universe at the different kinds of systems that are there, that the ones with simpler rules would somehow have simpler computational abilities. Well, to some extent that is definitely true. When the rules are simple enough, the system will do nothing interesting. For example, it will give an input, the input will just stay fixed and will not change throughout the evolution of the system and that is not a basis for doing a sophisticated computation.

For many years I studied what is out there in the computational universe. I was using Mathematica as a telescope to look and try to do the natural history of all these strange creatures that exist in the computational universe. And having done the natural history, try to classify them and then try to find general principles about what happens out in the computational universe.

One of the general principles I developed that I think is really an important general principle is what I call the principle of computational equivalence. What this principle has to do with is the following. When we look at all these different computational systems we can ask: How powerful are the computations that they are doing? And it could be that one system is, in a sense, a system with simpler rules, which would be always weaker in the power of the computation that it was doing.

But this principle of computational equivalence says that whenever you see a system whose behavior does not look obviously simple—is not repetitive, is not nested, and does not have any other obvious regularity—whenever you see a system that does not have obvious regularities, the system will tend to be equivalent in its computational sophistication, equivalent in its computational power. So that means that a system like this rule 30 system should be able to be just as powerful computationally as any other computational system or in particular, as any Turing machine, any CPU chip, whatever else.

What that then gets one started on is the question of: How does one figure out if that is true or not? In a sense this principle of computational equivalence is a very general kind of abstract principle at the beginning, but among other things like any good principle it makes a bunch of predictions.

One of its predictions is that out of these various simple systems that one sees, essentially any one of them that is not obviously simple in its behavior should be capable of universal computation. It should be possible to take that system and assemble what it does into being able to perform an arbitrary computation.

Figure 8 is a particular case where we now know that this is possible. This is the rule 110 cellular automaton. It is the cellular automaton that you reach in this sequence of possible cellular automata.

Figure 8.

Its rule is at the bottom there. This is what it does if you start it up in random initial conditions. When you first look at this it looks like it might be a bunch of particles interacting in some way. Perhaps it is a good metaphor for that. But it is also something where you could imagine that these are a bunch of signals propagating around doing logic and things like this.

What tends to be possible and was kind of a lot of work, is a tiresome process in many ways but it turns out to be possible, is to give kind of a formal proof that yes, indeed, you can assemble all those logic elements to actually make with this particular cellular automaton any computation you want to make. So this is a proof of the prediction of the principle of computational equivalence, that yes it is possible to take even one of the very simple systems that are out there in the computational universe and find that they are as computationally powerful as anything else. So that means that just this little rule is in a sense capable of as sophisticated a computation as anything else.

That has considerable significance when it comes to thinking about systems in nature because what we might have thought is that one of the great achievements of our civilization is the construction of CPU chips, being able to make these universal computers with CPU chips. But these CPU chips are complicated things. Millions of gates, all that kind of thing. They are not the sorts of things that we would expect to find just lying around in nature. That has been our traditional intuition of computation, that a CPU chip is a very special thing.

But what this principle of computational equivalence and what this evidence from rule 110 and so on suggest is that that intuition is not correct. That actually computation is something much more widespread. Because while we might not expect to find the million gate CPU chip just lying around in nature, we can readily expect to find things with rules that are like this rule 110 cellular automaton here just sort of lying around in nature.

What that means is that many systems in nature, in a sense, should be as sophisticated computationally as anything that we can build. So when we look at something like this rule 30 cellular automaton, what we are seeing here is something that is, in a sense, doing computation as powerfully as anything else we can find.

This fact has many implications. It explains the very observation that we view rule 30 for example as doing complicated things. When we study systems in science and theoretical science, there is always a kind of competition between us as theoreticians and the systems themselves—us, as observers of the systems, and the systems themselves just doing what they do. An idealization that is typically made in science is that the observers are, in a sense, computationally infinitely more powerful than the systems they are observing.

So that means, whatever the system does, we as observers of the system should be able to crush its computational effort. We should be able to take that system and reduce and figure out what the system is going to do by some method that does not involve all the effort that the system went to. It is kind of what happens in physics, for example, if you look at an idealized two-body problem of the Earth going around the Sun. If we want to know where the Earth is going to be a million years from now, we do not have to follow a million orbits, we just have to plug a number into a formula and immediately we know the answer. In a sense, we are reducing the computational effort that it is necessary to go through to find out the results of this computation.

The big thing that one realizes from this principle of computational equivalence and this whole A New Kind of Science (NKS) set of ideas is that the notion of computational reducibility is actually a fairly special case. That out there in the space of possible abstract systems, out there in the computational universe, a very large fraction of systems are actually doing much more complicated things that are in a sense computationally powerful and are in a sense computationally irreducible. There is really no way to work out what this system, for example, will do by any procedure that is much more efficient I think than just running the system and seeing what happens—that is the idea of computational irreducibility. That makes this system seem complex to us.

Now computational irreducibility has lots of consequences for computation because, for example, when it comes to studying systems in nature we might have had the idea that with our fancy computers and algorithms and all that kind of thing, we can always outrun what any system in nature will do. We can always just find an exact formula that will work out what the system will do. What this idea of computational irreducibility shows is that for very fundamental reasons that is not possible. That in a sense the idea of simulating systems in nature is a necessary idea. It is not something that is just convenient. It is something that is fundamentally necessary.

And that puts more pressure on us to find the right primitives representing natural systems in a way that fits in well with the kinds of computers that we actually use. Because we know we are going to have to do a lot of computational operations to find out what the natural system does. So those operations should be as simple as possible so that we get to do as many of them as efficiently as possible. In a sense, that forces us to think about the kinds of primitives that should exist, let us say in Mathematica, as ways to represent the natural world. Are they primitives that are well-matched with the kinds of things that actually go on in the natural world or not? And I would say that what I have seen from studying NKS and so on is that I am very pleased with the extent to which the kind of symbolic programming primitives that we have in Mathematica seem to map well in a very wide range of different kinds of computational models that seem to be relevant in studying the natural world.

I just want to say a few things about the implications of this realization. One is that computation is something that is all around us, that happens in all kinds of systems, that does not require any kind of special engineering to achieve. Also, one of the things that this principle of computational equivalence begins to suggest is a bulk notion of computation, much as the laws of thermodynamics begin to suggest a bulk notion of things like heat and so on, which might have been divided into a zillion different subcases. So this principle of computational equivalence begins to suggest that there is this bulk notion of an amount of computation that one can assign to all kinds of different physical, natural, perhaps social, etc., kinds of systems. And that is how one understands this idea of computational irreducibility.

Just to say a few things about what the implications of this might be, I will mention a few that I happen to think are fun right now. One example is in biology (Figure 9).

Figure 9.

For example with these simple cellular automata, there are now lots of people who are thinking about using one-dimensional cellular automata as an example for kids to learn what one might call precomputer science, kind of applying a simple algorithm and seeing what its consequences are. One of the things that is really great there is that one can say, okay apply the simple algorithm, see what comes out, and now here is at least one system in the natural world that you can see really does seem to work more or less according to that algorithm.

This particular example is of the mollusk shell as shown in Figure 10, which grows in a sort of one-dimensional fashion with a line of biological cells at the lip where the shell grows. It lays down pigment in what can be approximated as discrete steps. The pattern that it produces is something that looks rather like that rule 30 cellular automaton.

Figure 10.

I cannot explain why this particular textile-cone species of mollusk uses something like rule 30. But we can ask a more general question. If we look out at the mollusks of the Earth, what kinds of patterns do they produce? They all have the same basic idea of having a line of cells and the cells have certain interactions between them. What forms of patterns do they produce? And in a sense, what we are asking to do here, we can try and do predictive biology. We can say, given this basic model of the system having this line of cells, let us just assume the genetic program is kind of random, that it determines what the new pigment that is going to be laid down is.

If that was the case, what if we picked all possible programs consistent with that kind of simple model and saw what consequences those programs have? These turn out to be a bunch of simple, one-dimensional cellular automata and it is easy to find out what their consequences are. And what we see is that we would expect some things where the mollusks are just white, other things where they have stripes, other things where they have spots. And then we have a weird prediction, we say, there should also be mollusks that have these complicated tent-like patterns on them. So now we go and look at the mollusks of the Earth and lo and behold, that is what we see.

So in a sense what we have done here is found a predictive version of biology. What people traditionally say is that there cannot be a theory to the forms of current biological organisms; there can be no more theory to them than there can be a theory to human history, for example. That the details of what we see in biological organisms today must be determined by a long torturous history of biological evolution.

But in a sense, with this idea of abstract processes and computation, what that leads to for us is this notion that the mollusks of the Earth let us say, or the biological organisms of the Earth are kind of a sampling, a good approximation to what they are doing is they are sampling simple programs at random. They are kind of covering the space and we get to see the consequences of these programs played out in the morphologies and the other features of these organisms. It is like these things are just running programs and print the results of the programs on their shell. And we get to see the results of those programs. So that is actually quite a program of what one can call predictive biology, that one can start to do on the basis of this idea. It may or may not be correct.

The next one we are looking at seriously is leaf shapes as shown in Figure 11.

Figure 11.

There is great diversity in the shapes of possible leaves and I have a simple model that seems to explain a wide range of these kinds of leaves.

Okay, I will tell you a silly anecdote. When I was working on the book, I have this page of leaves that was just an array of images of different leaf shapes. And I was convinced that the book was going to be finished within a couple of months. Unfortunately I was having to make this page of leaves right in the middle of winter in Chicago, which is where I was then, thinking how on earth am I going to get images of leaves in the middle of winter because there are no leaves on the trees here? Fortunately, at that time there was a person who was working with the company who lived in Australia, who happened to be a few blocks from the Melbourne Botanical Gardens. And so I called him and said, “Could you just go and collect some leaves and put them in a FedEx envelope and send them to me?” People have commented on an excruciating number of detailed points about things in the NKS book, which is very nice to see because it means that people are actually reading it in great detail. But I have been waiting for the moment when some botanist says, “Why are these leaves a mixture of ones that were collected from California, (a few of them were collected in early days of the book when I was in California), from Illinois, and then these big Australian leaves?” But so far, nobody has said that, so I await that moment.

Anyway, the interesting thing here is that you can get a predictive model of biology that tries to say, what are the shapes of all possible leaves? So, for example, you can also have fun thinking about the shapes of all possible dinosaurs. You know, who would expect the stegosaurus with its funny plates on its back? I do not know how that works yet.

A couple of people have been working on skeleton structures based on NKS ideas of exploring the computational universe of possible forms. One of the things that you get to do then is to say, okay, here is the array of shapes including some very unexpected ones and we found this fossil and this fossil and this fossil. But you know there should also be one that is here. And it is not something that is like the traditional Darwinian style of saying there should be a missing link between here and here because there is sort of a continuous gradation. It is something where in the space of possible computations, there is potentially a very unexpected thing that happened and it should be there. So that is one of the applications of thinking about what is out there in the computational universe.

I will mention another one that is perhaps in a sense more bizarre. I am not going to go into this in tremendous detail. It has to do with physics.

Figure 12.

One of the questions that comes up when you start seeing something like Figure 12, where you have just that little rule that is there and then you realize that from that little rule you get this great richness of behavior that you see here, you immediately start to ask the ultimate question, which is: If you can make so much from so little, can one make the whole universe from little? And, in particular, could there perhaps be some simple set of rules that determines everything that happens in the universe?

And in a sense, if we take this idea of universal computation seriously, ultimately that should be the case. Ultimately any kind of system that we might look at should be able to represent what happens in the universe. It will be an issue whether the initial conditions that you have to specify for the universe are simple or not within that kind of system.

One thing you realize is that if you want to find simple rules for the universe, almost nothing that is familiar in our current universe will be immediately visible in those rules. Because in a sense the rules are too small, there is no room to put in the little piece that represents the muon, the number 3 that represents the dimensions of space, things like that. These things have to be all kind of mixed together. So you start thinking what are the possible, very fundamental, kind of computational-like systems? You can start just thinking about the space of all such possible systems as possible rules for the universe.

And that is a long story, much of it is in the NKS book, but my favorite systems to think about in this regard are networks, where essentially all that is specified is connectivity data. You have a bunch of nodes and all that you are saying is which node is connected to which other node. You do not say how far apart anything is. You do not say where anything is in some kind of embedding in space. You just say what the connectivity is. The remarkable fact, and a long story, but the remarkable fact is that from this very underlying, very combinatorial structure it is possible to have all sorts of common features of our universe as we know it emerge. And for example, it is the case that much as the second law of thermodynamics operates, much as the derivation of hydrodynamics operates, that many fluids that have a bunch of molecules bouncing around all obey the Navier-Stokes equations for continuous fluid flow, so similarly with certain constraints any system that is based on these network rules has certain conservation of dimension kinds of properties and certain microscopic randomness. It turns out that such a system must satisfy special relativity in certain limiting cases and must in general satisfy Einstein’s equations for general relativity. Which is a non-trivial, in my opinion, a very impressive and non-trivial consequence of something where the underlying rules are extremely simple.

So as we start thinking about exploring the computational universe and what computations are possible out there, the question comes up: If we start enumerating possible rules for, for example a system like these network kinds of things in Figure 13, could we find as we enumerate these rules, could we somehow find our actual universe out there?

Figure 13.

It could certainly be the case that our universe would be rule number 17, or our universe could be rule number , or our universe could be rule number . If we believe this kind of notion of universality, our universe must be somewhere out there in the space of possible rules.

And the question is: How simple will the rules be? I do not have any particular criterion to decide that, although it is a very fundamental fact about nature that the rules for nature are not as complicated as they might be. For example, the universe has perhaps a little less than particles in it. If the rules for the universe had different cases in them, we might reasonably expect that every one of those particles might choose to do a different thing. Yet what we know is that there is considerable order in the universe, that the rules are not that complicated. Most of the particles choose to follow the same kind of rules all the time. And so the rules are simple compared to, in a sense, the size of the universe. How simple they are we do not know. We do not have a criterion. There is not yet a criterion by which we might guess how simple the rules might be.

But it is kind of an interesting thing if we start searching the computational universe, to ask the question.

As we do that, as we search the computational universe, where might our universe, our actual physical universe be in the space of the possible computational universes?

It is a wonderful application of Mathematica actually. It is a fairly sophisticated, fairly high-tech thing that involves feeding in a possible rule for the universe to see what it does. Many rules for the universe are completely stupid. One can say immediately, this is not our universe. No notion of time, space, expands exponentially in a trivial way forever, etc. What you really want to know, for example, is given some potential universe, what are the laws that operate in this universe and are they the same laws that we know, whether it is the standard model gauge invariance or general relativity, or whatever else. Are they the same laws that we know from existing physics?

And that is a non-trivial thing to determine because this notion of computational irreducibility says you start the thing off, you start it running. It may do all kinds of complicated things and it may be very unclear what its global rules actually are. And in fact what we have to hope for are pockets of computational reducibility, where we will be able to kind of get our hands on the thing and find out that it actually corresponds to the laws that we traditionally know about.

That has turned into this big enterprise of essentially doing automated theorem proving and things like that and doing a whole bunch of graph theory and combinatorics. It is a wonderful Mathematica system using gridMathematica, and so on to try and do these searches that involve basically finding out what we can prove for candidate universes. It is kind of automating the process of being a natural scientist or a theoretical natural scientist. Given this set of rules, what can we determine from that about laws of this universe?

It has been going rather well and there are some nice technology spin-offs, which will show up in Mathematica. One of the consequences of finding out that our universe is one of these universes out there in the computational universe is that it really grounds the notion of computation. If our universe is one of these things out in the computational universe, we know that is all that is there. We cannot start arguing, oh well, computation as we know it right now is not really everything that is relevant in the universe, there might be some special rule-number thing, there might be some hyper-computation thing, there might be some other weird thing going on. We will be able to say, no that absolutely is not the case, everything that happens is just determined by this particular computational model.

It may not be easy to work out the consequences of this model. From the model, the question “is warp drive possible?” or something may be in effect an undecidable question, in the sense that there is no finite computation that can determine whether there exists some configuration of masses, etc., etc., etc. that allows you to do this or that.

From the point of view of grounding our notion of computation, this is important. And from the point of view of knowing that we have got the right primitives for computation, it will certainly be an interesting thing to be able to find the fundamental laws of physics of our universe in these terms. It may be a little disappointing. We may be saying, my gosh, I wish our universe had more interesting rules, but we will know what the actual rules are.

One of the things that comes up, that is a little bit analogous that I might mention and then I am going to talk about some quite different things, is the question of what happens in another case of where out there in the computational universe are the things that we know and like? The case I will talk about is mathematics.

All of mathematics is actually based on a fairly small set of axioms. Figure 14 basically shows all the axioms now in use in all common areas of mathematics.

Figure 14.

So they are fairly small. And from these small axioms there grow millions of theorems that exist in the literature of mathematics. Some of which have a property very much like computational irreducibility, that even though the theorem may be simple to state, like Fermat’s last theorem or something like that, the proof of the theorem may be long to generate and there may be no short way to prove that theorem.

Well one of the things that is interesting is this is mathematics as it exists, these are the particular axiom systems that have been chosen through the historical development of mathematics from Babylonian times and so on. But we can start enumerating axiom systems from mathematics, just selecting axiom systems, we are building arbitrary fields of mathematics. Each axiom system corresponds to a field of mathematics.

Figure 15.

So Figure 15 is an example of what happens when you do that. Each row here is a different axiom system. Each column represents a theorem. So this is an ultimately idealized, ultimately desiccated form of mathematics, where the possible axioms for the different fields of mathematics go down the left, the possible theorems go across the top, and there is a black dot whenever a particular theorem is true for a particular system.

We can then ask the question: The axiom systems for mathematics as we currently know them and like them, where do they lie in the space of all possible axiom systems? What you might have imagined, what you might have thought is that they would be either at the very beginning or they would be very far away.

Let me give you one example where I know the answer about how far away the thing is.

Figure 16.

Figure 16 shows some standard axioms for Boolean algebra. One of the things we can ask ourselves is: If we were to just enumerate possible axiom systems out there in the abstract space of possible mathematics, where would Boolean algebra lie? I just enumerated possible axiom systems—kind of just like going out and searching for possible universes. It is the kind of thing that you would think was just completely crazy, just looking at all possible axiom systems and finding whether out there you find Boolean algebra.

Well it turns out that in the case of Boolean algebra, the axiom system roughly, you find Boolean algebra. And it is an adventure in automated theorem proving to show that the little axiom system really is Boolean algebra. There is a proof, and this is soon going to be immediately doable in Mathematica. But that is a different story. What is interesting here is that this Boolean algebra that we know is out there in the computational universe of possible things at around the axiom system.

So this notion of “just go out there in the computational universe and find things” is I think an important notion that is very useful for many different purposes. One place you can use this is in modeling in natural science. You can say, okay, I have this system in nature, let me try and see whether I can find the model out there in the computational universe that is a good representation, a good abstract idealization of this particular system in nature. And there are many examples that one can give of cases where that is possible.

Traditionally when we do statistics or something we say there is going to be a model that is described by this formula. Let us tweak the parameters so that it comes up with the best fit to the particular data that we have. What we are asking here is something more ambitious. We are saying, we have this phenomenon. Now go out and look at all possible abstract processes of certain kinds and see which one is the best fit to what happens. And that will be a good idealized representation and we may then understand that the mechanism corresponds in some way.

With this discovery that very simple programs are sufficient to reproduce very complicated behavior, it makes sense to do this kind of a search. Because without that, if you saw anything complicated in nature, it would be absolutely hopeless to imagine that this search in the space of the computational universe would find anything that actually corresponds to the particular phenomenon we were looking for.

One place where we can start to explore the computational universe is to find models for things. Another place where we can do this is in trying to find things that are useful for technology. In a sense what we want to do is a big mining expedition of existing technology. If you look at the history of technology, it is largely characterized by saying, okay, go and look in the natural world and find something that is useful for something. Whether it is iron or whether it is something about the fact that you can make radio waves and use that for communication or whether it is liquid crystals for displays or whatever else, you get to go and forage the natural world and find things that are useful for technology.

So the thing that we now realize is that in this abstract computational universe, we get to do the same kind of thing. We can go out in this abstract computational universe and just start searching, foraging for different possible computational processes and programs that are useful to us.

And so for example one thing we might do is we might identify the program in Figure 17 as being useful for making randomness.

Figure 17.

Now one of the things that happens here is that by our traditional methods of engineering, we would never have constructed Figure 17 as a way to make randomness. This is not something that is accessible by our traditional human methods of engineering. But it is something that we can just find out there in the computational universe.

And there are many other examples of this. In fact, we have been using this kind of idea for many years in some areas of Mathematica to just search spaces of possible algorithms and find algorithms for things.

But this is something which we can now start to think about and do much more generally. And this offers a natural approach to computation, searching this computational universe of naturally occurring computations out there.

If we look at our computations that we tend to construct from an engineering point of view, we might have an iterative computation, that is essentially repetitive in its behavior. Or we might have some more modern, recursive, divide-and-conquer algorithm that is kind of nested in its behavior.

But one of the things that is interesting to ask is: When we look for things which are kind of optimal for their particular purpose, are they in fact simple computations? Or are they simple looking computations, or not?

Figure 18.

Figure 18 shows pictures of sorting networks. And these first two pictures are kind of standard sorting algorithms. The last three pictures are the actual optimal sorting networks found by exhaustive search for particular sizes. What we see there is that they do not look particularly simple. They are out there in the computational universe but they are not things we would have found with engineering.

And so, we can ask a more abstract version of that question. We can look at all possible Turing machines.

Figure 19 is an example of a few Turing machines that do the not terribly difficult operation of adding 1 to a binary number. You put in at the top the binary representation of a number, you run the Turing machine, and at the end it stops with 1 added to that number. And so of the simplest possible Turing machines there are three different types that succeed in adding 1 to a number.

Figure 19.

But we can then ask the questions: If we look at the possible Turing machines, what kinds of things do they compute? When there are different Turing machines that compute the same thing, which ones do it most efficiently? What is the form, what is the kind of structure of the computation that they do? What you find is that for some computations the best, the most efficient kind of Turing machines are ones that do the computation in a systematic way. But there are also many, many cases where the best in terms of efficiency are ones that do their computations in a very irregular, non human-understandable, very non human-constructible kind of way. And that is an example of just going out there and mining the computational universe to find things that are useful for our purposes.

I think that one of the key things that we will see in the future of computation is this effort to mine the computational universe, to take the core essence of computation that one can represent among other things with symbolic programming, and so on, that one can use this very raw essence of computation and be able to do things like just mine these arbitrary computational systems to find things that are useful, to find the things that will be easy to do by mining the computational universe.

It is kind of fun to realize that there are lots of different things, operations that have traditionally seemed very hard to do, which we can now fairly easily imagine being able to find. We have no idea how to engineer the things. But we can imagine doing a search and finding a pretty good example that can do a pretty good job, whether it is making hash codes, constructing things in nanotechnology, doing bioengineering kinds of things, making error-correcting codes of more complicated kinds than have been made, or doing compression. There are all sorts of areas where we can just imagine mining the computational universe to find programs that exist out there and are useful for these purposes.

As we find these non human-understandable kinds of things out there, much will change in the way that computation happens in the world. We should realize that lots more things are doing computation than we imagined. Lots of things in nature, lots of things in social systems and so on are in effect doing computation. And we get to interact with these things only with the realization that there is computational irreducibility involved in most of these processes.

Here is a good example of how computational irreducibility operates in the world of the future: right now when we have a transportation system, the traditional thing is that we have trains that operate on time on a sort of periodic schedule. In the world of the future with everything being computational, you get to realize that there are sensors everywhere and you have these little taxis which arrive just in time and can compute, all these different people want to go from here to there and there are enough sensors to know all of that. But then when you zoom out and look at the system in operation, it will look like something more complicated. It will look like something that is very hard to determine what is going to happen in it. No doubt the algorithms that are being used here, the good algorithms, will be ones that are just found by searching the computational universe rather than ones that tend to be engineered. Because among other things, the ones that tend to be engineered tend to not be very robust against the kinds of things that can happen in the real world.

I need to wrap up. But I just wanted to show you Figure 20 as an example of one recent thing that we did, which is kind of fun.

Figure 20.

It does not really exist yet, but it will exist in about a month. So do not tell people about it yet, but you can tell them about it in a month. This is kind of an example of a place where one can search the computational universe for something that turns out to be useful. In a sense it is an absurd and frivolous example, whose origins were in fact quite frivolous. The idea was, we know that things like cellular automata and other kinds of simple programs can readily produce complex and visually appealing patterns. They can produce beautiful visual forms.

One of the things that happened after NKS was first released was that people started using simple programs also to generate musical forms, as well as auditory forms, as well as visual forms. And at some point I realized that one of the places that is really useful in practice is the almost frivolous use of cellphone ringtones. Because that is a place where everybody wants something appealing and elegant but they want it to be different. So it is a place where if you can mine the computational universe and find all these different things, that is a useful thing to do.

I did not think this was going to work. I did not think this was going to be nearly as easy as it turned out to be. Let me just explain what the idea is. In a sense, any musical composition, any one of these simple programs produces and defines something with an internal logic. There is a particular rule and you are seeing the consequences of that particular rule and it has a certain internal logic to what it does. And that is in a sense what you want of a decent musical composition, that you have a certain integrity and a certain internal logic to it.

So the idea here is that we are playing out the consequences of some simple rule and rendering it as a musical composition. Now as a practical matter there is a fair amount of sophistication in how that rendering is done. But what we are doing here is basically just selecting out from the computational universe. Figure 21 shows you how this works with this particular rule number of a cellular automaton.

Figure 21.

And Figure 22 shows variations of that with, for example, different rules.

Figure 22.

Figure 22 is a cellular automaton on its side. We start with the initial conditions and go across with time. The height of a particular cell determines the frequency of a note, just like a musical score. Various algorithms pick out how the cells in the cellular automaton should be mapped into different musical instruments.

There is some sophistication in how that is done. For example, there are roughly 40 different kinds of scales. Let us pick a random Japanese scale, for example Figure 23, and let us play this piece again.

Figure 23.

Every time I press this button, the system is basically searching the computational universe to find a simple program that satisfies certain aesthetic criteria and then renders it as a musical form. The way that rendering is done depends on how the thing is mapped into musical scales and what instruments are used. But what is happening here is we are hearing pieces of the computational universe. And we are using the fact that in the space of possible programs there are many that are musically interesting, maybe one in a thousand that turn out to be useful for some particular style of music or another.

WolframTones, tones.wolfram.com, is a good webMathematica venture. It is completely built in webMathematica, running right now on a cluster of computers. And hopefully enough people will be interested in it that it will actually strain the computers when the site goes live. But the practicalities involve being able to take these musical forms and download them to cellphones.

What I wanted to say about this was that this is an example of rather unexpectedly going out and mining the computational universe to find things which are useful. If you want to have a musical composition made that has certain features, right now you would have to go out and hire a composer to do that. But this is an example of a place where you can do mass customization for artistic purposes. You can have the creativity come from just searching this computational universe of possible programs to find things. And that is another feature of computation that I think is going to be extremely prevalent, this mass customization of things, whether it is mass customization of musical forms for cellphones, mass customization for medical purposes, or mass customization of algorithms or particular compression tasks. It will be possible to create a new thing by just going out and searching, by doing a mining expedition rather than constructing by engineering purposes.

Stephen Wolfram
Founder and CEO
Wolfram Research, Inc.
s.wolfram@wolfram.com
www.wolframscience.com